DS Processing

In this tutorial, we demostrate how to do standard DS processing with the Moraine package.

import numpy as np
import zarr
from matplotlib import pyplot as plt
import colorcet

from moraine.utils_ import is_cuda_available
if is_cuda_available():
    import cupy as cp
    from cupyx.scipy.ndimage import uniform_filter

import moraine as mr

Load rslc stack

if is_cuda_available():
    rslc = cp.asarray(zarr.open('../../data/rslc.zarr',mode='r')[:])
    print(rslc.shape)

(2500, 1834, 17)

Apply ks test

if is_cuda_available():
    rmli = cp.abs(rslc)**2

az_half_win = 5
r_half_win = 5
az_win = 2*az_half_win+1
r_win = 2*r_half_win+1

if is_cuda_available():
    p = mr.ks_test(rmli,az_half_win=az_half_win,r_half_win=r_half_win)

Select SHPs

if is_cuda_available():
    is_shp = (p < 0.05) & (p >= 0.0)
    del p

if is_cuda_available():
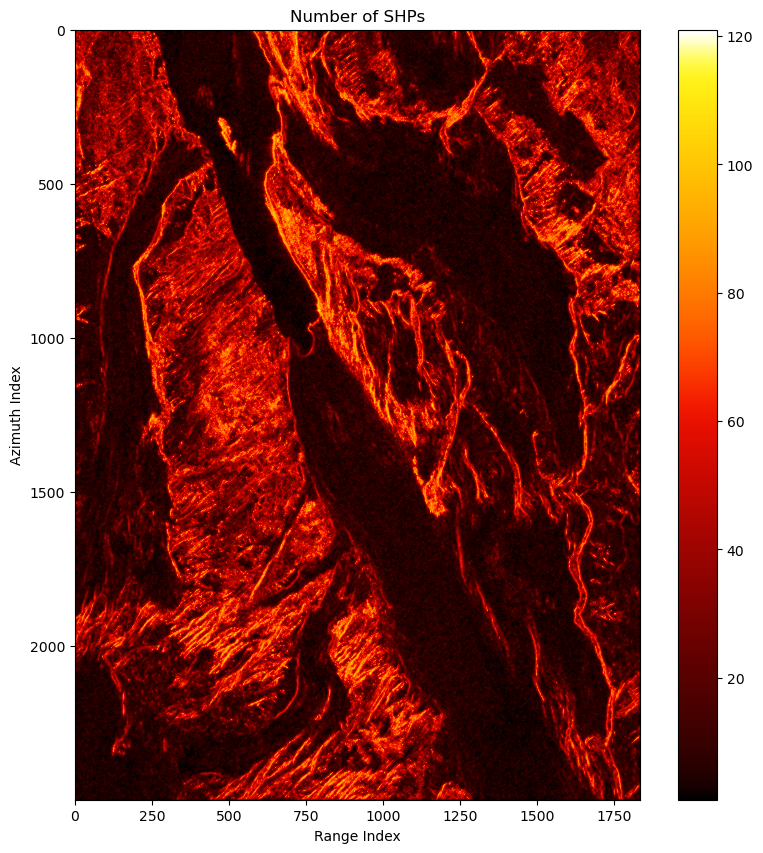
    shp_num = cp.count_nonzero(is_shp,axis=(-2,-1))

if is_cuda_available():
    fig, ax = plt.subplots(1,1,figsize=(10,10))
    pcm = ax.imshow(cp.asnumpy(shp_num),cmap=colorcet.cm.fire)
    ax.set(title='Number of SHPs',xlabel='Range Index',ylabel='Azimuth Index')
    fig.colorbar(pcm)
    fig.show()

Select DSs

Here we select DSs candidate as pixels have more than 50 brothers.

if is_cuda_available():
    is_ds_can = shp_num >= 50
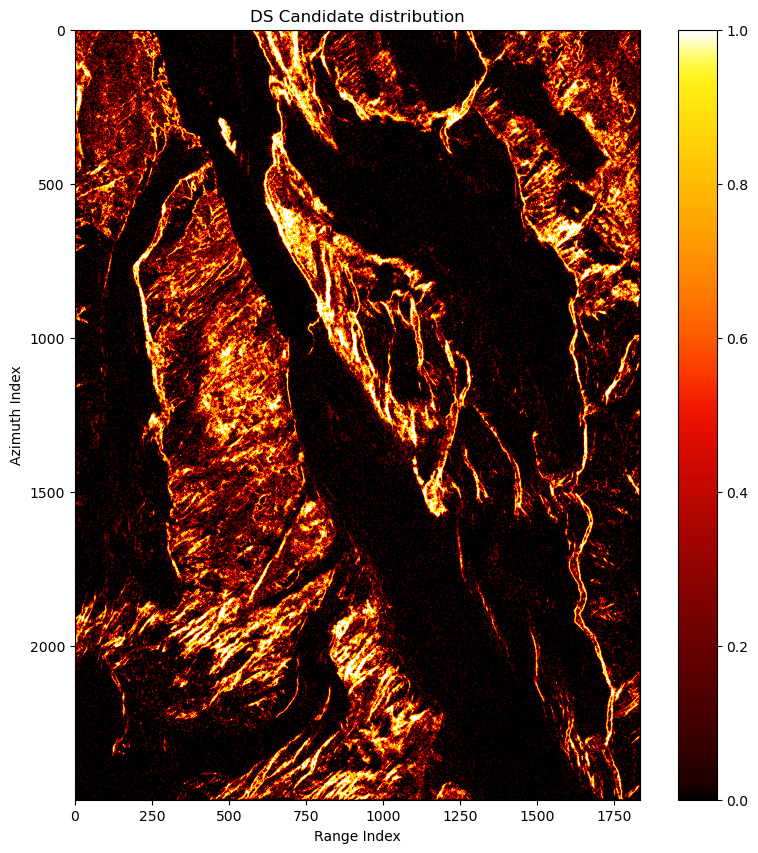
    del shp_num

The number of DSs:

if is_cuda_available():
    cp.count_nonzero(is_ds_can)

The DSs distribution:

if is_cuda_available():
    fig, ax = plt.subplots(1,1,figsize=(10,10))
    pcm = ax.imshow(cp.asnumpy(is_ds_can),cmap=colorcet.cm.fire)
    ax.set(title='DS Candidate distribution',xlabel='Range Index',ylabel='Azimuth Index')
    fig.colorbar(pcm)
    fig.show()

Estimate coherence matrix

In order to save memory, here we only estimate coherence matrix on selected DSs:

if is_cuda_available():
    ds_can_is_shp = is_shp[is_ds_can]
    ds_can_idx = cp.stack(cp.where(is_ds_can),axis=-1)
    ds_can_coh = mr.emperical_co_pc(rslc,ds_can_idx,ds_can_is_shp)
    del is_shp

Plot the average coherence matrix:

if is_cuda_available():
    ds_can_ave_coh = abs(ds_can_coh).mean(axis=0)
    ds_can_ave_coh_uncompressed = mr.uncompress_coh(ds_can_ave_coh)
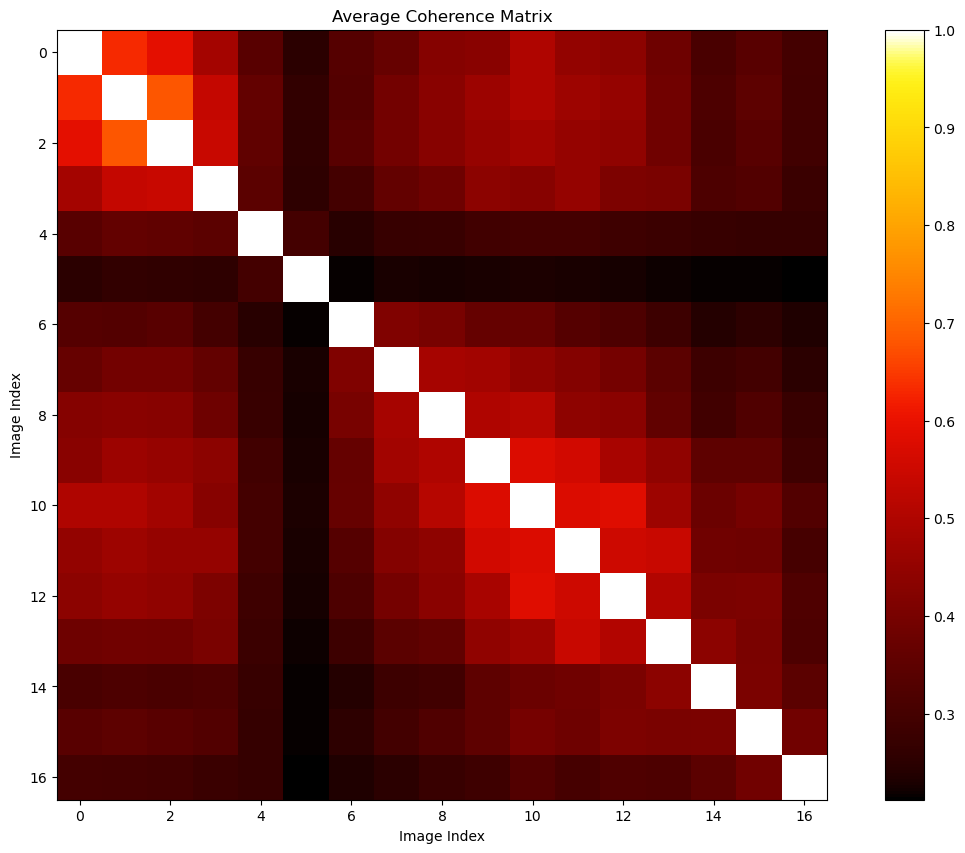
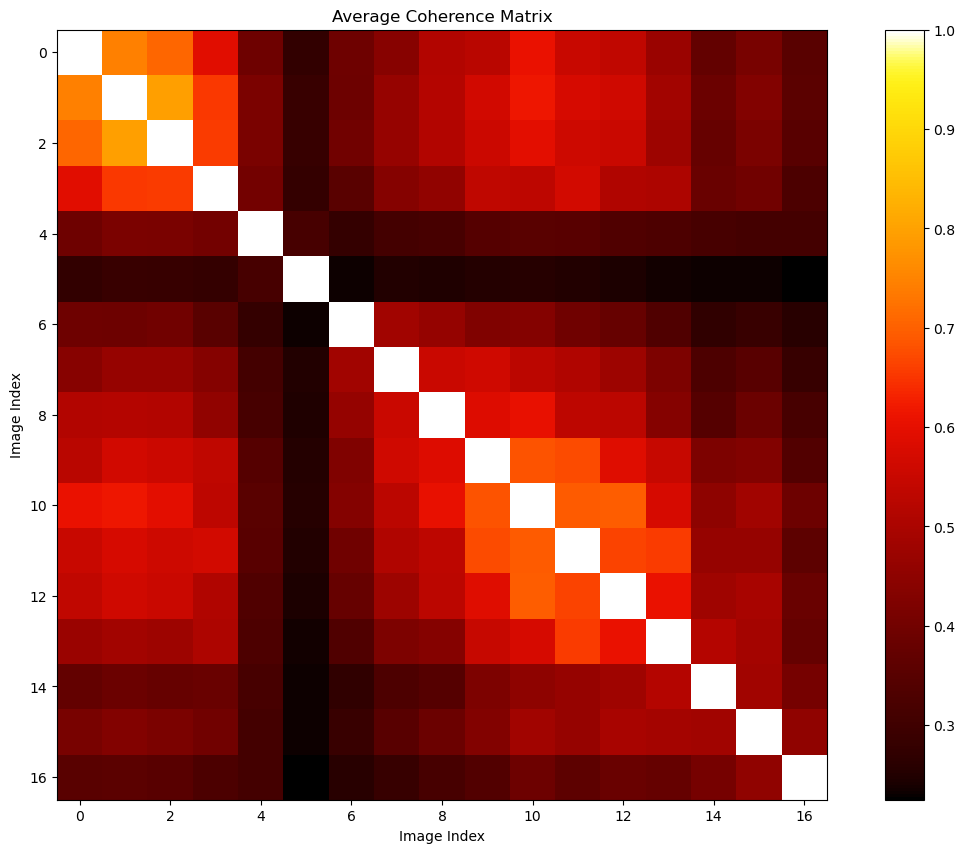
    print(ds_can_ave_coh.shape,ds_can_ave_coh_uncompressed.shape)

(136,) (17, 17)

fig, ax = plt.subplots(1,1,figsize=(15,10))
pcm = ax.imshow(ds_can_ave_coh_uncompressed.get(),cmap=colorcet.cm.fire)
ax.set(title='Average Coherence Matrix',xlabel='Image Index',ylabel='Image Index')
fig.colorbar(pcm)
fig.show()

The coherence between the 5-th SLC and other SLC are bad. We may consider removing this image.

Phase linking

Here we apply the EMI method:

if is_cuda_available():
    ds_can_ph, ds_can_emi_quality = mr.emi(ds_can_coh)
    print(ds_can_ph.shape, ds_can_emi_quality.shape)

(732727, 17) (732727,)

if is_cuda_available():
    ds_can_emi_quality_2d = cp.empty_like(is_ds_can,dtype=ds_can_emi_quality.dtype)
    ds_can_emi_quality_2d[:] = cp.nan
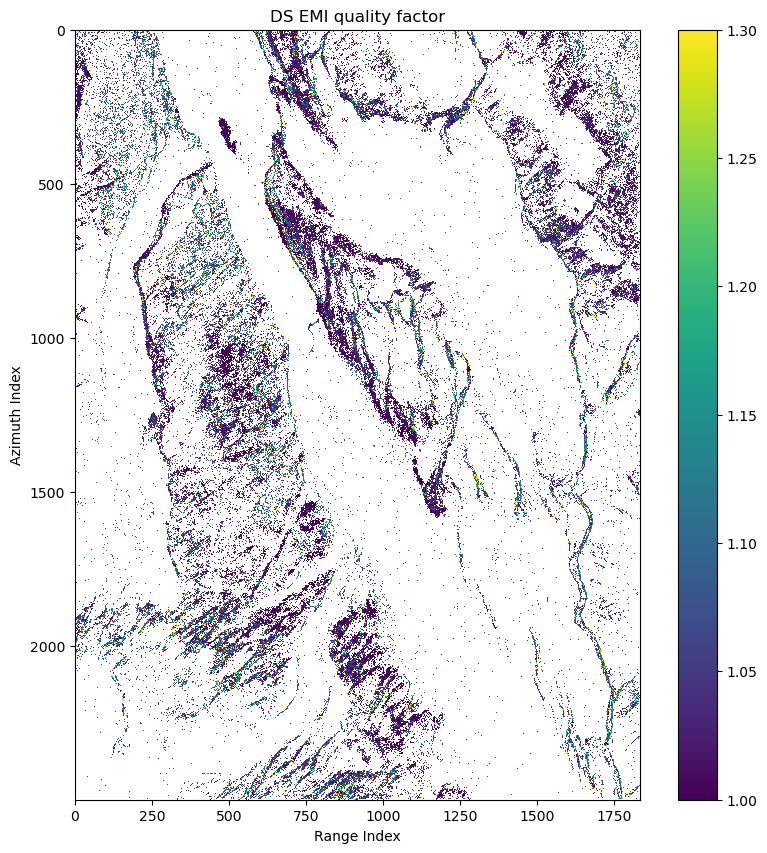
    ds_can_emi_quality_2d[is_ds_can] = ds_can_emi_quality

if is_cuda_available():
    fig, ax = plt.subplots(1,1,figsize=(10,10))
    pcm = ax.imshow(cp.asnumpy(ds_can_emi_quality_2d),interpolation='nearest',vmin=1,vmax=1.3)
    ax.set(title='DS EMI quality factor',xlabel='Range Index',ylabel='Azimuth Index')
    fig.colorbar(pcm)
    fig.show()

if is_cuda_available():
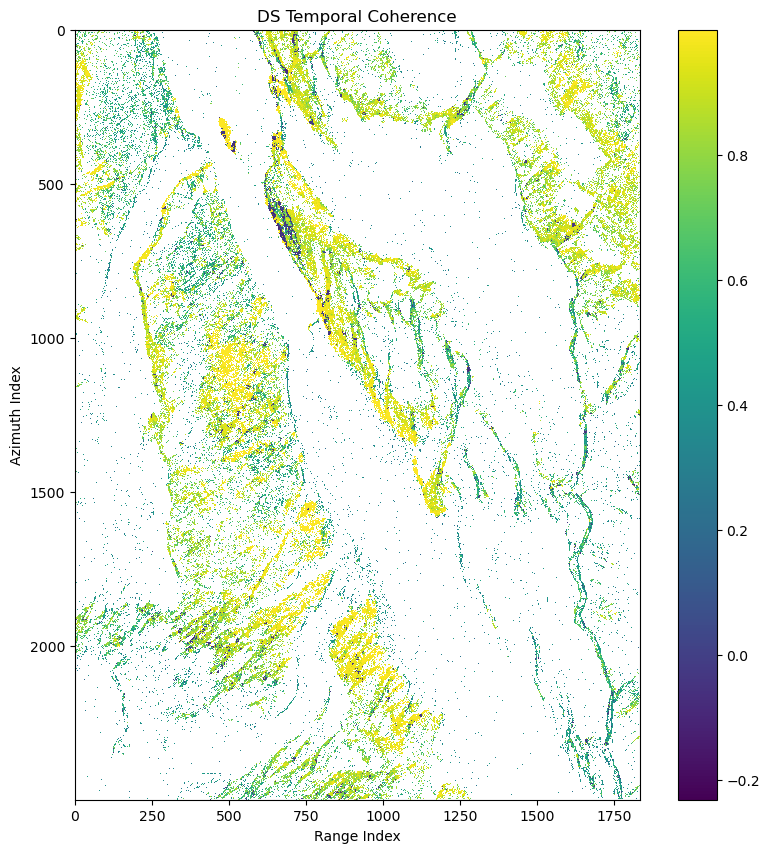
    ds_can_temp_coh = mr.ds_temp_coh(ds_can_coh,ds_can_ph)
    print(ds_can_temp_coh.shape)

(732727,)

if is_cuda_available():
    ds_can_temp_coh_2d = cp.empty_like(is_ds_can,dtype=ds_can_temp_coh.dtype)
    ds_can_temp_coh_2d[:] = cp.nan
    ds_can_temp_coh_2d[is_ds_can] = ds_can_temp_coh
    fig, ax = plt.subplots(1,1,figsize=(10,10))
    pcm = ax.imshow(cp.asnumpy(ds_can_temp_coh_2d),interpolation='nearest')
    ax.set(title='DS Temporal Coherence',xlabel='Range Index',ylabel='Azimuth Index')
    fig.colorbar(pcm)
    fig.show()

Refine DS candidate

Here we select DS candidate based on EMI quality factor and temporal coherence:

if is_cuda_available():
    _is_ds_can_refined = (ds_can_emi_quality>=1.0) & (ds_can_emi_quality <1.2) & (ds_can_temp_coh > 0.7) & (ds_can_temp_coh <= 1.0)

if is_cuda_available():
    ds_can_refined_idx = ds_can_idx[_is_ds_can_refined]
    is_ds_can_refined = cp.zeros_like(is_ds_can,dtype=bool)
    is_ds_can_refined[ds_can_refined_idx[:,0],ds_can_refined_idx[:,1]] = True

if is_cuda_available():
    ds_can_refined_coh = ds_can_coh[_is_ds_can_refined]
    ds_can_refined_ph = ds_can_ph[_is_ds_can_refined]
    ds_can_refined_coh.shape

Plot the average coherence matrix and refined DS candiate distribution:

if is_cuda_available():
    ds_can_refined_ave_coh = abs(ds_can_refined_coh).mean(axis=0)
    ds_can_refined_ave_coh_uncompressed = mr.uncompress_coh(ds_can_refined_ave_coh)
    fig, ax = plt.subplots(1,1,figsize=(15,10))
    pcm = ax.imshow(cp.asnumpy(ds_can_refined_ave_coh_uncompressed),cmap=colorcet.cm.fire)
    ax.set(title='Average Coherence Matrix',xlabel='Image Index',ylabel='Image Index')
    fig.colorbar(pcm)
    fig.show()

if is_cuda_available():
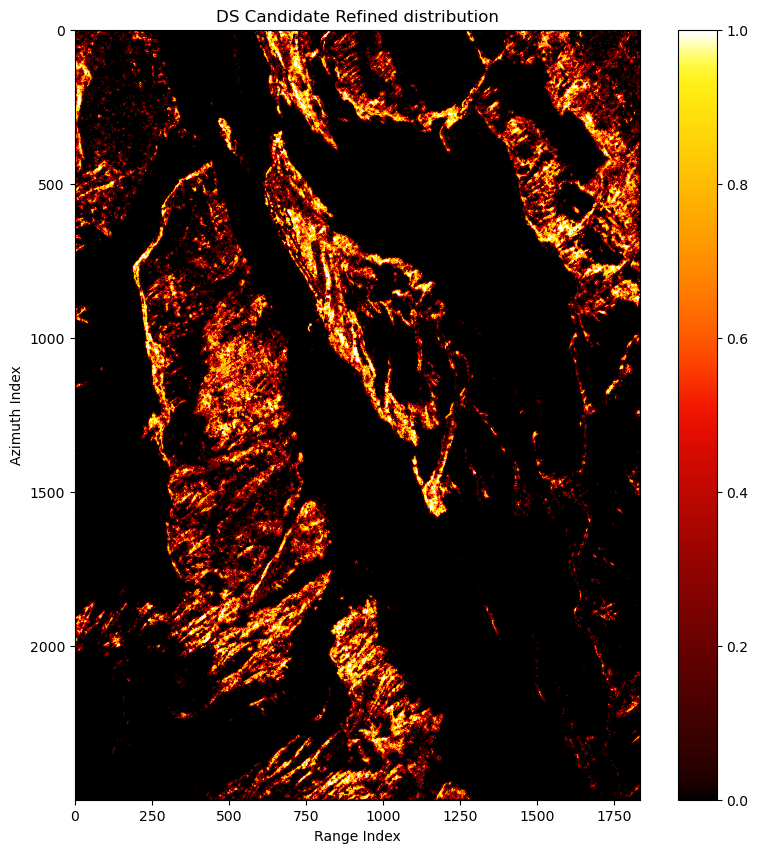
    fig, ax = plt.subplots(1,1,figsize=(10,10))
    pcm = ax.imshow(cp.asnumpy(is_ds_can_refined),cmap=colorcet.cm.fire)
    ax.set(title='DS Candidate Refined distribution',xlabel='Range Index',ylabel='Azimuth Index')
    fig.colorbar(pcm)
    fig.show()

We find the coherence matrix gets better and noisy pixels are moved.

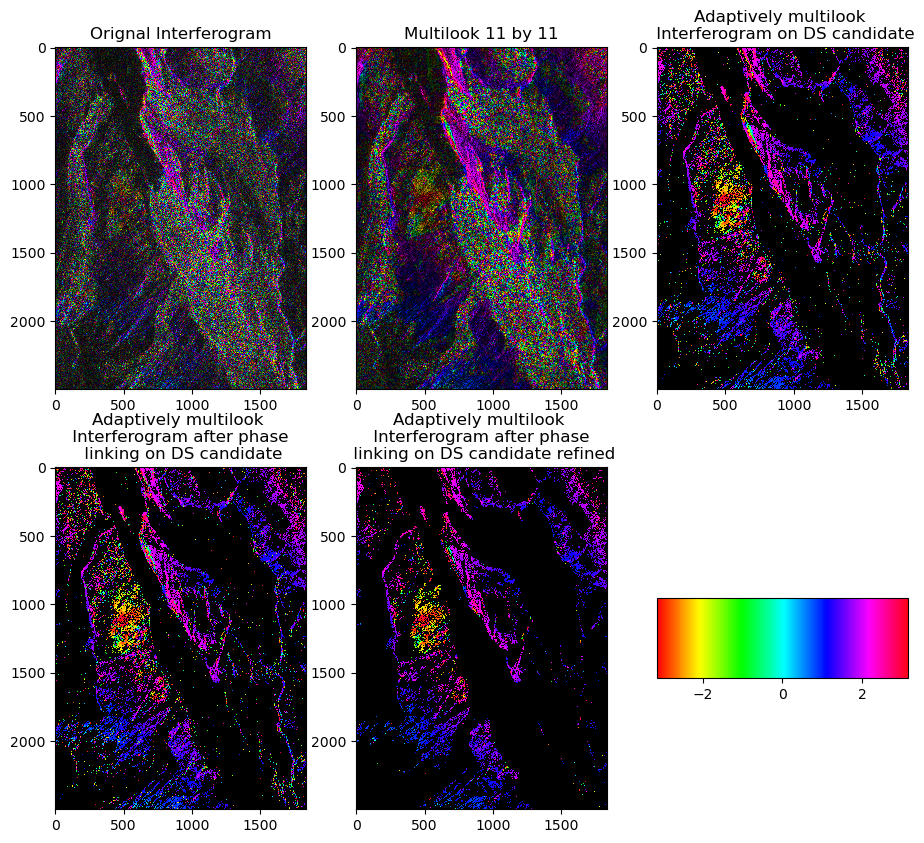
Show the interferogram improvement

Here we select one interferogram to show the improvement:

ref_image = 1
sec_image = 10

1 look interferogram:

if is_cuda_available():
    diff_2d = rslc[:,:,ref_image]*rslc[:,:,sec_image].conj()

Multilook interferogram:

if is_cuda_available():
    ml_diff_2d = uniform_filter(diff_2d,size=(az_win,r_win))

Adaptive multilook interferogram on DS candidates:

tnet = mr.TempNet.from_bandwidth(rslc.shape[2])
image_pair_idx = tnet.image_pairs_idx(ref=ref_image,sec=sec_image)

if is_cuda_available():
    ds_can_diff_2d = cp.empty_like(diff_2d)
    ds_can_diff_2d[:] = cp.nan
    ds_can_diff = ds_can_coh[:,image_pair_idx]
    ds_can_diff_2d[is_ds_can] = ds_can_diff

Adaptive multilook interferogram after phase linking on DS candidates:

if is_cuda_available():
    ds_can_diff2_2d = cp.empty_like(diff_2d)
    ds_can_diff2_2d[:] = cp.nan
    ds_can_diff2 = ds_can_ph[:,ref_image]*ds_can_ph[:,sec_image].conj()
    ds_can_diff2_2d[is_ds_can] = ds_can_diff2

Adaptive multilook interferogram after phase linking on refined DS candidates:

if is_cuda_available():
    ds_can_refined_diff_2d = cp.empty_like(diff_2d)
    ds_can_refined_diff_2d[:] = cp.nan
    ds_can_refined_diff = ds_can_refined_ph[:,ref_image]*ds_can_refined_ph[:,sec_image].conj()
    ds_can_refined_diff_2d[is_ds_can_refined] = ds_can_refined_diff

The plot background:

if is_cuda_available():
    plot_bg = rmli[:,:,0]
    plot_bg = cp.asnumpy(plot_bg)
    plot_bg = np.nan_to_num(plot_bg)
    alpha = mr.bg_alpha(plot_bg)

Plot:

if is_cuda_available():
    f,axes = plt.subplots(2,3,figsize=(11,10))
    #axes[-1,-1].remove()
    axes = axes.flatten()
    xlabel = 'Range Index'
    ylabel = 'Azimuth Index'
    pcm = axes[0].imshow(cp.asnumpy(cp.angle(diff_2d)),alpha=alpha,interpolation='nearest',cmap='hsv')
    axes[1].imshow(cp.asnumpy(cp.angle(ml_diff_2d)),alpha=alpha,interpolation='nearest',cmap='hsv')
    axes[2].imshow(cp.asnumpy(cp.angle(ds_can_diff_2d)),alpha=1,interpolation='nearest',cmap='hsv')
    axes[3].imshow(cp.asnumpy(cp.angle(ds_can_diff2_2d)),alpha=1,interpolation='nearest',cmap='hsv')
    axes[4].imshow(cp.asnumpy(cp.angle(ds_can_refined_diff_2d)),alpha=1,interpolation='nearest',cmap='hsv')
    for ax in axes:
        ax.set(facecolor = "black")
    axes[0].set(title='Orignal Interferogram')
    axes[1].set(title=f'Multilook {az_win} by {r_win}')
    axes[2].set(title=f'Adaptively multilook \n Interferogram on DS candidate')
    axes[3].set(title=f'Adaptively multilook \n Interferogram after phase \n linking on DS candidate')
    axes[4].set(title=f'Adaptively multilook \n Interferogram after phase \n linking on DS candidate refined')

    f.colorbar(pcm,cax=axes[5],orientation='horizontal')
    axes[5].set_aspect(2)