pl

Phase Linking

import numpy as np
import zarr
import moraine as mr
from moraine.utils_ import is_cuda_available
if is_cuda_available():
    import cupy as cp
from matplotlib import pyplot as plt

EMI

---

source

emi

 emi (coh:numpy.ndarray, ref:int=0)

	Type	Default	Details
coh	ndarray		complex coherence metrix,dtype cupy.complex
ref	int	0	index of reference image in the phase history output, optional. Default: 0
Returns	tuple		estimated phase history ph, dtype complex; quality (minimum eigvalue, dtype float)

# #| export
# def emi(coh:np.ndarray, #complex coherence metrix,dtype cupy.complex
#         ref:int=0, #index of reference image in the phase history output, optional. Default: 0
#        )-> tuple[np.ndarray,np.ndarray]: # estimated phase history `ph`, dtype complex; quality (minimum eigvalue, dtype float)
#     xp = get_array_module(coh)
#     coh_mag = xp.abs(coh)
#     coh_mag_inv = xp.linalg.inv(coh_mag)
#     min_eigval, min_eig = xp.linalg.eigh(coh_mag_inv*coh)
#     min_eigval = min_eigval[...,0]
#     # min_eig = min_eig[...,0]
#     min_eig = min_eig[...,0]*min_eig[...,[ref],0].conj()

#     return min_eig/abs(min_eig), min_eigval

emi is a phase estimator base on Eigendecomposition-based Maximum-likelihood-estimator of Interferometric phase (EMI) (Ansari, De Zan, and Bamler 2018) phase linking method.

Ansari, Homa, Francesco De Zan, and Richard Bamler. 2018. “Efficient Phase Estimation for Interferogram Stacks.” IEEE Transactions on Geoscience and Remote Sensing 56 (7): 4109–25. https://doi.org/10.1109/TGRS.2018.2826045.

The amplitude of coh should range between 0 and 1 and the phase of coh should be the interferometric phase. The returned phase is also complex but the amplitude is setted to 1. The quality factor is a measure for the inadequacy of EMI’s model that adding real-valued dyadic for calibration of real coherence matrix which is generally poorly estimated. It is supposed to larger than 1 and smaller means better.

Important

This function is deprecated as estimate coherence for all pixels are not necessary. Please use emperical_co_pc instead.

Example: Complex coherence matrix from a stack of 17 SLC images:

rslc = zarr.open('../../data/rslc.zarr/','r')[:]

# SHP selection
az_half_win = 5; r_half_win = 5
az_win = 2*az_half_win+1; r_win = 2*r_half_win+1

rmli = np.abs(rslc)**2

p = mr.ks_test(rmli,az_half_win=az_half_win,r_half_win=r_half_win)
is_shp = p < 0.05

# Select DS candidate
shp_num = np.count_nonzero(is_shp,axis=(-2,-1))
is_ds_can = shp_num >= 50

ds_can_is_shp = is_shp[is_ds_can]
ds_can_idx = np.stack(np.where(is_ds_can),axis=-1)
ds_can_coh = mr.emperical_co_pc(rslc,ds_can_idx,ds_can_is_shp)
print(ds_can_coh.shape)

(740397, 136)

ds_can_ph, ds_can_emi_quality = emi(ds_can_coh)
print(ds_can_ph.shape, ds_can_emi_quality.shape)

(740397, 17) (740397,)

ds_can_emi_quality_2d = np.empty_like(is_ds_can,dtype=ds_can_emi_quality.dtype)
ds_can_emi_quality_2d[:] = np.nan
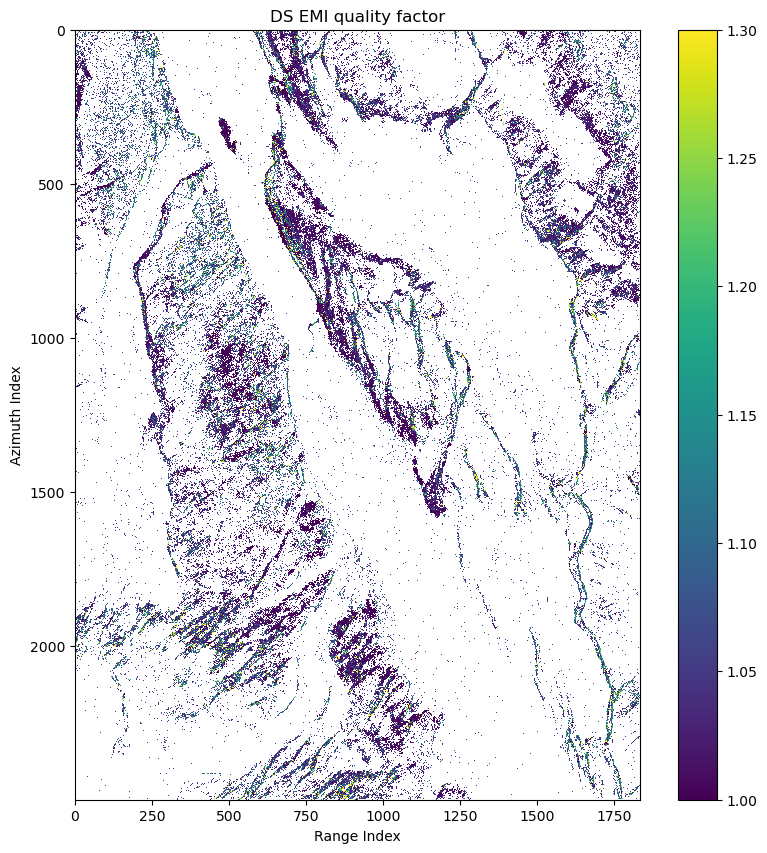
ds_can_emi_quality_2d[is_ds_can] = ds_can_emi_quality

fig, ax = plt.subplots(1,1,figsize=(10,10))
pcm = ax.imshow(ds_can_emi_quality_2d,interpolation='nearest',vmin=1,vmax=1.3)
ax.set(title='DS EMI quality factor',xlabel='Range Index',ylabel='Azimuth Index')
fig.colorbar(pcm)
fig.show()

cupy.ndarray is also supported:

if is_cuda_available():
    ds_can_ph_, ds_can_emi_quality_ = emi(cp.asarray(ds_can_coh))

Temporal Coherence for Distributed Scatterer

---

source

ds_temp_coh

 ds_temp_coh (coh:numpy.ndarray, ph:numpy.ndarray,
              image_pairs:numpy.ndarray=None, block_size:int=128)

	Type	Default	Details
coh	ndarray		complex coherence metrix, np.complex64 or cp.complex64
ph	ndarray		complex phase history, np.complex64 or cp.complex64
image_pairs	ndarray	None	image pairs, all image pairs by default
block_size	int	128	the CUDA block size, only applied for cuda

This function estimate the temporal coherence of DSs as

\[\gamma = \frac{1}{N_{IP}} \operatorname{Re} \sum_{n, k \in IP} e^{i\phi_{nk}} e^{-i(\theta_n-\theta_k)}\]

Where \(\phi_{nk}\) is the phase of complex coherence matrix, \(\theta_{n}\) is the phase after phase linking, \(IP\) is the image pairs, \(N_{IP}\) is the number of image pairs.

If all image pairs are considered, then it is exactly same temporal coherence defined in (Ferretti et al. 2011):

Ferretti, Alessandro, Alfio Fumagalli, Fabrizio Novali, Claudio Prati, Fabio Rocca, and Alessio Rucci. 2011. “A New Algorithm for Processing Interferometric Data-Stacks: SqueeSAR.” IEEE Transactions on Geoscience and Remote Sensing 49 (9): 3460–70. https://doi.org/10.1109/TGRS.2011.2124465.

\[\gamma = \frac{2}{N^2-N} \operatorname{Re} \sum_{n=1}^{N} \sum_{k=n+1}^{N} e^{i\phi_{nk}} e^{-i(\theta_n-\theta_k)}\]

rslc = zarr.open('../../data/rslc.zarr/','r')[:]

# SHP selection
az_half_win = 5; r_half_win = 5
az_win = 2*az_half_win+1; r_win = 2*r_half_win+1

rmli = np.abs(rslc)**2
p = mr.ks_test(rmli,az_half_win=az_half_win,r_half_win=r_half_win)
is_shp = p < 0.05

# Select DS candidate
shp_num = np.count_nonzero(is_shp,axis=(-2,-1))
is_ds_can = shp_num >= 50

ds_can_is_shp = is_shp[is_ds_can]
ds_can_idx = np.stack(np.where(is_ds_can),axis=-1)
ds_can_coh = mr.emperical_co_pc(rslc,ds_can_idx,ds_can_is_shp)
ds_can_ph = emi(ds_can_coh)[0]
print(ds_can_coh.shape,ds_can_ph.shape)

(740397, 136) (740397, 17)

ds_can_temp_coh = ds_temp_coh(ds_can_coh,ds_can_ph)
print(ds_can_temp_coh.shape)
if is_cuda_available():
    ds_can_temp_coh_cp = ds_temp_coh(cp.asarray(ds_can_coh), cp.asarray(ds_can_ph))
    np.testing.assert_array_almost_equal(ds_can_temp_coh, ds_can_temp_coh_cp.get())

(740397,)

ds_can_temp_coh_2d = np.empty_like(is_ds_can,dtype=ds_can_temp_coh.dtype)
ds_can_temp_coh_2d[:] = np.nan
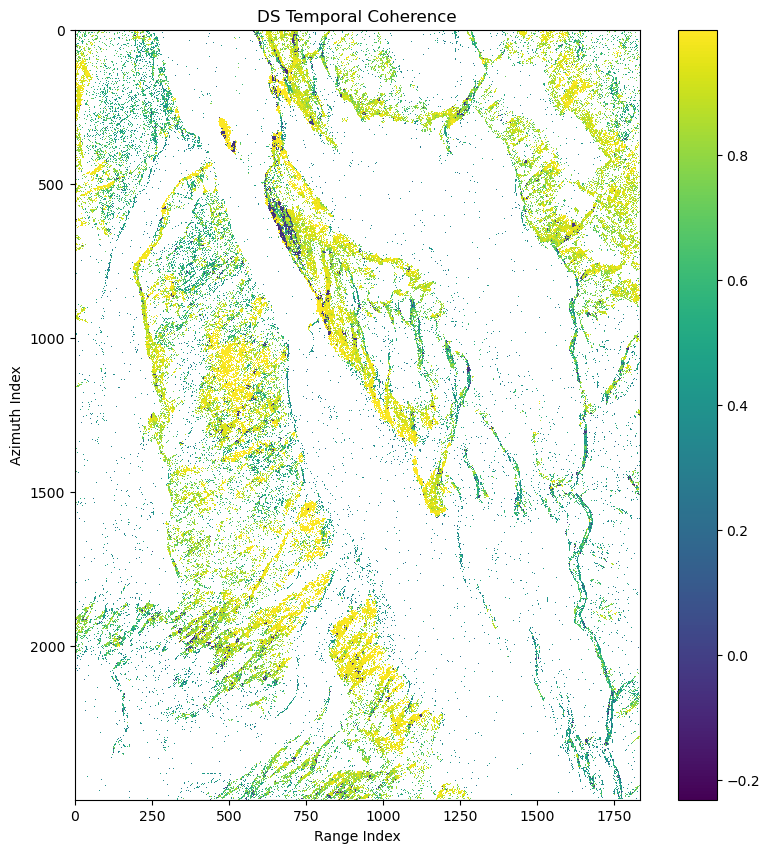
ds_can_temp_coh_2d[is_ds_can] = ds_can_temp_coh

fig, ax = plt.subplots(1,1,figsize=(10,10))
pcm = ax.imshow(ds_can_temp_coh_2d,interpolation='nearest')
ax.set(title='DS Temporal Coherence',xlabel='Range Index',ylabel='Azimuth Index')
fig.colorbar(pcm)
fig.show()

---

source

emperical_co_emi_temp_coh_pc

 emperical_co_emi_temp_coh_pc (rslc:numpy.ndarray, idx:numpy.ndarray,
                               pc_is_shp:numpy.ndarray,
                               batch_size:int=1000)

	Type	Default	Details
rslc	ndarray		rslc stack, dtype:‘np.complex64’
idx	ndarray		index of point target (azimuth_index, range_index), dtype: np.int32, shape: (n_pc, 2)
pc_is_shp	ndarray		shp bool, dtype:‘np.bool’
batch_size	int	1000

emperical_co_emi_temp_coh_pc is the combination of emperical_co_pc, emi and ds_temp_coh. But it does not return the coherence matrix as the full coherence matrix may be too big to fill the memory. The functions provide the batch_size options to do the processing in batch.

rslc = zarr.open('../../data/rslc.zarr/','r')[:]

# SHP selection
az_half_win = 5; r_half_win = 5
az_win = 2*az_half_win+1; r_win = 2*r_half_win+1

rmli = np.abs(rslc)**2
p = mr.ks_test(rmli,az_half_win=az_half_win,r_half_win=r_half_win)
is_shp = p < 0.05

# Select DS candidate
shp_num = np.count_nonzero(is_shp,axis=(-2,-1))
is_ds_can = shp_num >= 50

ds_can_is_shp = is_shp[is_ds_can]
ds_can_idx = np.stack(np.where(is_ds_can),axis=-1)

ds_can_ph, ds_can_emi_quality, ds_can_t_coh = emperical_co_emi_temp_coh_pc(rslc,ds_can_idx,ds_can_is_shp,batch_size=1000)

ds_can_coh_ = mr.emperical_co_pc(rslc,ds_can_idx,ds_can_is_shp)
ds_can_ph_, ds_can_emi_quality_ = emi(ds_can_coh_)
ds_can_t_coh_ = ds_temp_coh(ds_can_coh_,ds_can_ph_)
np.testing.assert_array_equal(ds_can_ph,ds_can_ph_)
np.testing.assert_array_equal(ds_can_emi_quality,ds_can_emi_quality_)
np.testing.assert_array_equal(ds_can_t_coh,ds_can_t_coh_)