Pixel Quality Metrics

import numpy as np
import zarr
import moraine as mr
from moraine.utils_ import is_cuda_available
if is_cuda_available():
    import cupy as cp
from matplotlib import pyplot as plt

---

source

temp_coh

 temp_coh (intf:numpy.ndarray, rslc:numpy.ndarray,
           image_pairs:numpy.ndarray=None, block_size:int=128)

Estimation of temporal coherence.

	Type	Default	Details
intf	ndarray		complex interferograms/coherence metrix, dtype cp/np.complex64, shape 2D(pc) or 3D(ras)
rslc	ndarray		complex rslc/phase history, dtype cp/np.complex64, shape 2D(pc) or 3D(ras)
image_pairs	ndarray	None	image pairs
block_size	int	128	the CUDA block size, only applied for cuda

This function estimate the temporal coherence of as

\[\gamma = \frac{1}{N_{IP}} \left| \sum_{n, k \in IP} e^{i\phi_{nk}} e^{-i(\theta_n-\theta_k)} \right| \]

Where \(\phi_{nk}\) is the phase of complex interferogram/coherence matrix, \(\theta_{n}\) is the phase of rslc or phase after phase linking, \(IP\) is the image pairs, \(N_{IP}\) is the number of image pairs.

If all image pairs are considered, then it is:

\[\gamma = \frac{2}{N^2-N} \left| \sum_{n=1}^{N} \sum_{k=n+1}^{N} e^{i\phi_{nk}} e^{-i(\theta_n-\theta_k)} \right| \]

This function applies to both raster data and point cloud data, an example for pc data is the estimation of temporal coherence for distributed scatterers after phase linking:

rslc = zarr.open('../../data/rslc.zarr/',mode='r')[:]

# SHP selection
az_half_win = 5; r_half_win = 5
az_win = 2*az_half_win+1; r_win = 2*r_half_win+1

rmli = np.abs(rslc)**2
p = mr.ks_test(rmli,az_half_win=az_half_win,r_half_win=r_half_win)
is_shp = p < 0.05

# Select DS candidate
shp_num = np.count_nonzero(is_shp,axis=(-2,-1))
is_ds_can = shp_num >= 50

ds_can_is_shp = is_shp[is_ds_can]
ds_can_idx = np.stack(np.where(is_ds_can),axis=-1)
ds_can_coh = mr.emperical_co_pc(rslc,ds_can_idx,ds_can_is_shp)
ds_can_ph = mr.emi(ds_can_coh)[0]
print(ds_can_coh.shape,ds_can_ph.shape)

(732727, 136) (732727, 17)

ds_can_temp_coh = temp_coh(ds_can_coh,ds_can_ph)
if is_cuda_available():
    ds_can_temp_coh_cp = temp_coh(cp.asarray(ds_can_coh), cp.asarray(ds_can_ph))
    np.testing.assert_array_almost_equal(ds_can_temp_coh, ds_can_temp_coh_cp.get())

ds_can_temp_coh_2d = np.empty_like(is_ds_can,dtype=ds_can_temp_coh.dtype)
ds_can_temp_coh_2d[:] = np.nan
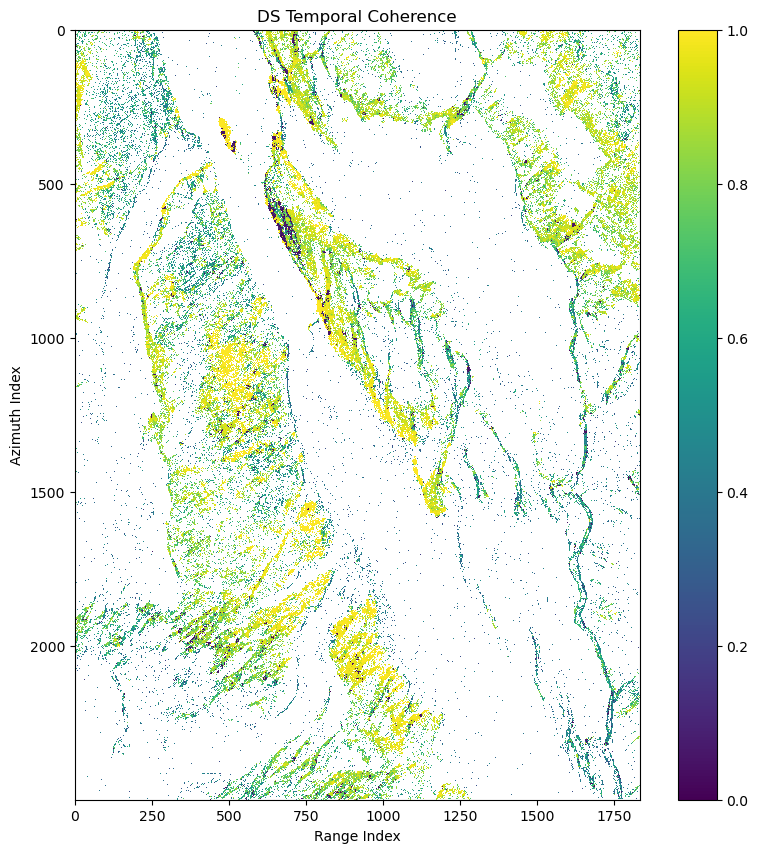
ds_can_temp_coh_2d[is_ds_can] = ds_can_temp_coh

fig, ax = plt.subplots(1,1,figsize=(10,10))
pcm = ax.imshow(ds_can_temp_coh_2d,interpolation='nearest',vmin=0.0,vmax=1.0)
ax.set(title='DS Temporal Coherence',xlabel='Range Index',ylabel='Azimuth Index')
fig.colorbar(pcm)
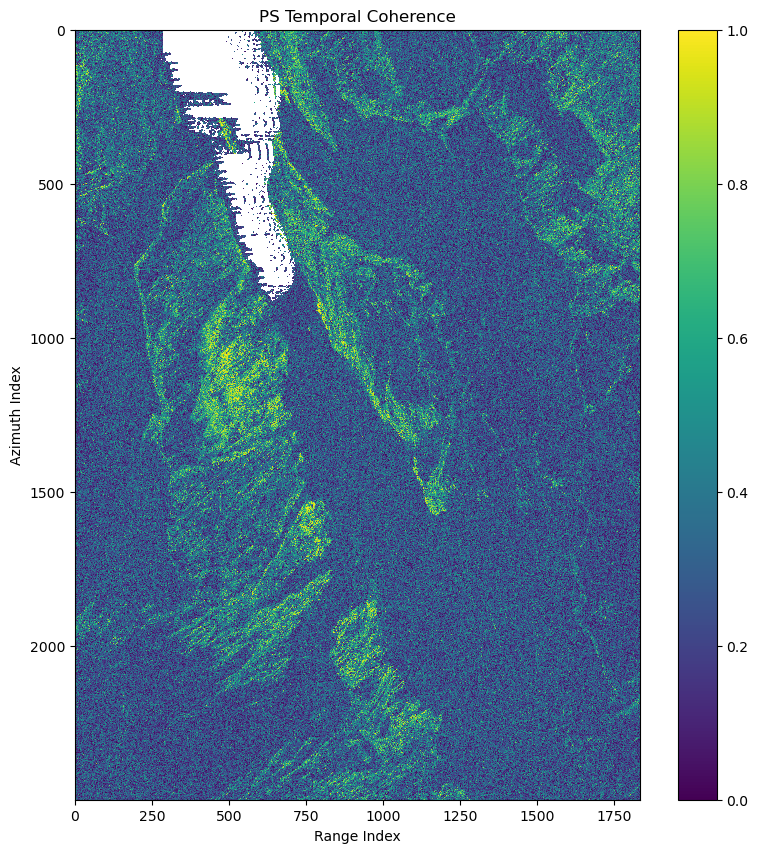
fig.show()

The example for raster data is the estimation of temporal coherence for selection of PS candidates with n2f:

rslc = zarr.open('../CLI/raw/rslc.zarr/',mode='r')[:]
intf = zarr.open('../CLI/dl/n2f_intf.zarr',mode='r')[:]
image_pairs = mr.TempNet.from_bandwidth(rslc.shape[-1],1).image_pairs

ps_temp_coh = temp_coh(intf,rslc,image_pairs)

or with gpu:

rslc_cp = cp.asarray(rslc)
intf_cp = cp.asarray(intf)
ps_temp_coh_cp = temp_coh(intf_cp,rslc_cp,image_pairs)
ps_temp_coh = ps_temp_coh_cp.get()

fig, ax = plt.subplots(1,1,figsize=(10,10))
pcm = ax.imshow(ps_temp_coh,interpolation='nearest',vmin=0.0,vmax=1.0)
ax.set(title='PS Temporal Coherence',xlabel='Range Index',ylabel='Azimuth Index')
fig.colorbar(pcm)
fig.show()